Measurement results close to limit values must be provided with a measurement uncertainty statement by laboratories accredited to DIN EN ISO/IEC 17025.
As a result, those who have to monitor compliance with such limit values are increasingly confronted with these measurement uncertainty statements. This then often leads to questions such as:
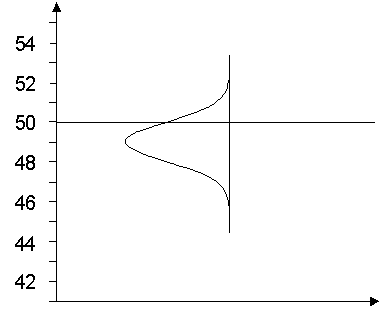
"Is 51 really significantly more than 50?"
These or similar questions are then asked of the analysts. The answer to this question depends, of course, on the level of measurement uncertainty. What would the answer be, then, if we assume that the measurement uncertainty range includes the limit value?
For the sake of simplicity, let us assume that the measured values are normally distributed. Then the estimation of the measurement uncertainty allows us to estimate with which probability a limit value is exceeded or not reached. Then we could have, for example, the following situation:
 from [1]
from [1]
If we want to give a scientifically correct answer, we come to the following conclusion (see also [2]):
"The probability that the true value of the concentration of the analyte in the object of study falls below the limit is estimated at 68%, and the probability that it exceeds it at 32%."
However, this statement usually cannot satisfy the questioner.
So we need to have a clear approach on how to deal with measurement uncertainty in compliance assessment.
If compliance with or exceeding of limit values is reported, the underlying decision rule must also be stated according to DIN EN ISO/IEC 17025.
It is obvious to hold the person responsible for setting the limit value, i.e. the quality target for a particular product, accountable for this. Often, however, these persons are not familiar with issues of measurement uncertainties, so they would do well to seek the assistance of persons with analytical expertise.[1]
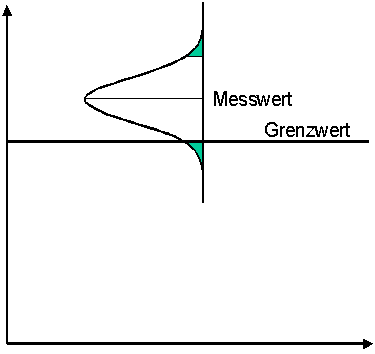
Option 1:
A limit value is exceeded when the measured value and the specified measurement uncertainty are above the limit value
 (from [1])
(from [1])
This procedure involves the risk that a wrong decision is made, i.e. that a value is accepted which is actually higher than the limit value. This risk is borne by the monitoring authority. It is obvious to use this procedure if the monitored person must be proven to have exceeded the limit value with a high degree of probability. The burden of proof therefore lies with the monitor.
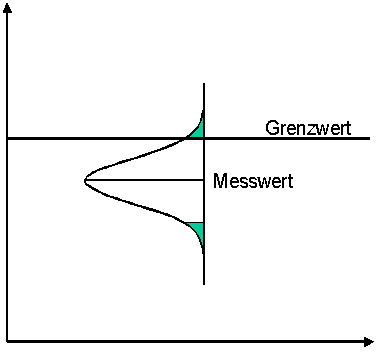
Option 2:
The limit value is considered to be complied with if the measured value is below the limit value by more than the specified measurement uncertainty.
 (from [1])
(from [1])
Here, too, there is a risk of incorrect evaluation. A measured value that is actually below the limit value is evaluated as an exceedance. The risk is now entirely on the side of the monitored party. In many cases, a monitored party has the burden of proof that its product complies with certain limit values. Then this methodology would be appropriate.
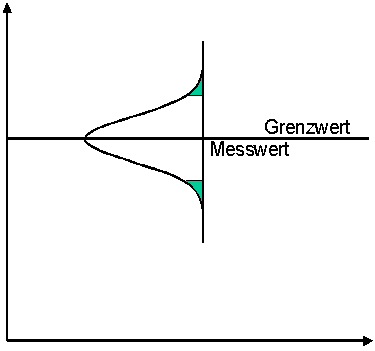
Option 3:
There is also a middle way. In this case, a measured value is evaluated as exceeding the limit value exactly when the measured value itself is above the limit value. The measurement uncertainty then plays no role in the evaluation.
 (from [1])
(from [1])
The risk of the wrong decision is shared.
The risk of a wrong decision cannot be avoided. However, there is the question of who bears this risk and, of course, there is also the question of the size of the risk. This risk can be quantified via the measurement uncertainty. Therefore, it is also extremely important that measurement uncertainties are correctly estimated. It is then in the interest of the person who has to bear the risk to limit this risk and thus to set limits for a permissible measurement uncertainty. Of course, these must also be realistic. It is not in anyone's interest if unrealistically small measurement uncertainties are specified that cannot be complied with in reality.
It is also essential that the framework conditions for the measurement uncertainty estimation are clearly defined. This includes the following aspects in particular:
- the confidence level must be defined and specified with the measurement uncertainty. A 95 % level, i.e. an expanded measurement uncertainty with the coverage factor 2, is common here. The "true value" is then expected with a probability of 95 % within the measurement uncertainty range.
- both precision and trueness should be included in the estimation of measurement uncertainty.
The Wastewater Ordinance [3] stipulates in § 6 that the limit values already take into account the measurement uncertainties of the analyses and sampling methods. This "legal dodge" thus establishes the sharing of the risk and the non-observance of the measurement uncertainty. The risk that is shared is open upwards. It is only limited by the fact that with the stipulation of certain analytical methods in the annex of the Wastewater Ordinance, a certain quality of analysis can be assumed. However, this in itself is no guarantee for small measurement uncertainties. Proficiency tests show this very clearly.
The Drinking Water Ordinance [4] and the underlying EU Directive 2020/2184 [5] contain requirements for the limit of determination and the uncertainty of measurement and, as with wastewater, the indication that the limits include the uncertainty of measurement.
If it is already a problem to develop a reasonable understanding of measurement uncertainty in the laboratory, it is much more difficult for customers. Educational work is therefore necessary.
In Sweden, a flyer was developed by SP for this purpose. It has been translated by the Federal Institute for Materials Research and Testing and is freely available to all interested parties [7].
Above all, it is important that the measurement uncertainty is not interpreted as a quality criterion for a laboratory. Rather, it must be checked in each case whether the measurement uncertainties stated by the laboratory are sufficient for the intended purpose of the analysis or not.
Competition between laboratories on the basis of measurement uncertainties would only result in these being systematically underestimated by laboratories, and the intended purpose of the uncertainty statement would thus be extremely jeopardized.
[1] Koch, M.: Messunsicherheit und Grenzwerte. Vom Wasser 103, 7-10 (2005)
[6] Koch, M.: Messunsicherheit in der Trinkwasseranalytik - Erkenntnisse aus Ringversuchen. Bundesgesundheitsbl Gesundheitsforsch Gesundheitsschutz 49, 1027-1033 (2006).

